3.1 Problemas de programación no lineal
Planteamiento del problema de Programación No Lineal.
El objeto de las siguientes secciones es definir una serie de conceptos relacionados con el problema general de programación no lineal, así como el estudio de las relaciones existentes entre cada uno de ellos y la solución de dicho problema.
Los conceptos que estudiaremos serán los siguientes:
Punto estacionario, en la sección 3.
Punto minimax, íntimamente relacionado con el concepto de dualidad, y que se estudiará en la sección 4.
Veremos que, en general, será más directa la demostración de la suficiencia de estas condiciones para asegurar que tenemos una solución del problema que la de la necesariedad de las mismas, para las que habrá que imponer condiciones de regularidad sobre las restricciones del problema, que llamaremos cualificaciones de restricciones. En esta sección se enuncian varias cualificaciones de restricciones y se estudia la relación entre ellas. En general, los resultados que se obtienen generalizan los dados en la sección anterior para los problemas con restricciones de igualdad, en el sentido de la existencia de condiciones de primer orden que implican a las primeras parciales de la función de Lagrange asociada al problema, y condiciones de segundo orden que suponen convexidad de ciertas funciones.
Un problema general de programación no lineal consiste en encontrar los valores de ciertas variables que maximizan o minimizan una función dada, dentro de un conjunto definido por una serie de restricciones de desigualdad, de forma que no hay aseguradas condiciones de linealidad ni sobre la función a optimizar ni sobre las funciones que definen el conjunto dentro del cual buscamos dicho óptimo.
donde:
y son ambas al menos de clase dos en todo su dominio.
El conjunto de oportunidades X es el conjunto en el cual maximizamos la función, es decir, la intersección entre el dominio de las funciones del problema y el conjunto determinado por las restricciones. Así,
donde
X = { x ∈ D / g(x) ≤ b },
b = (b1 ,…, bm).
Este tipo de problemas es muy representativo de las circunstancias en las que se desenvuelve la actividad económica. Normalmente, se dispone de cantidades limitadas de recursos, pero sin la obligación de emplearlas en su totalidad, si ello no resultase adecuado. Por consiguiente, es posible pensar en soluciones factibles y óptimas que no saturen necesariamente todas las restricciones, dejando un excedente inutilizado del recurso cuya disponibilidad limitan.
Se debe tener en cuenta sin embargo, en relación con el problema formulado, que el sentido de las desigualdades (≤) es únicamente cuestión de convenio. Una restricción con la desigualdad contraria puede reducirse a una del tipo anterior sin más que multiplicar por (-
1). Por otra parte, una restricción de igualdad puede reemplazarse por dos de desigualdad, por ejemplo, g(x) = b se convierte en g(x) ≤ b y –g(x) ≤ –b. O bien puede ser tratada directamente, sin restringir el signo del multiplicador correspondiente.
En ocasiones, para que el problema sea económicamente significativo, es necesario que las variables instrumentales sean no negativas, es decir, x ≥ 0. Más adelante en este capítulo, daremos un tratamiento específico a estas restricciones.
Asociadas al problema de maximización, podemos definir la siguiente función, muy importantes en lo que sigue:
Función de Lagrange L:
L : D × Rm+ → R
L(x, ë) = f(x) – ët[g(x) – b] 1,
donde ë ∈ Rm+ es el vector de multiplicadores asociado al bloque de restricciones del problema, también denominados multiplicadores de Kuhn-Tucker.
Dado un vector b ∈ Rm, si llamamos x0(b) a la correspondiente solución del problema de programación no lineal, se puede demostrar, análogamente a lo que vimos en el caso con restricciones de igualdad, que, para cada j = 1, …, m, anterior, una disminución del valor de bj originaría un aumento del valor de la función objetivo en el máximo, para un conjunto de oportunidades que es un subconjunto del de partida, lo que estaría en contradicción con que x0 fuera el máximo del problema original.
Al objeto de analizar en profundidad las propiedades del problema de programación no lineal, será necesario en algunos casos distinguir entre las restricciones que se verifican con igualdad en el óptimo y las que se verifican con desigualdad estricta. Así, diremos que la restricción gi(x) ≤ bi es activa en un punto factible x0 (o que x0 satura dicha restricción), si verifica gi(x0)= bi.
Ejemplos de Programación No Lineal
Ejemplo N° 1
A una compañía le cuesta c UM por unidad fabricar un producto. Si la compañía cobra p UM por unidad de producto, los clientes pedirán unidades. Para maximizar las ganancias, ¿qué precio tendría que poner la compañía?
Solución
La variable de decisión de la empresa es p
Dado que la ganancia de la empresa es , la empresa querrá resolver el siguiente problema de maximización sin restricción:
Ejemplo N° 2
Si se utilizan K unidades de capital y L unidades de trabajo, una compañía puede producir KL unidades de un bien manufacturado. Se puede conseguir el capital a 4 UM/unidad y el trabajo a 1 UM/unidad. Se dispone de un total de 8 UM para contratar capital y trabajo. ¿Cómo puede la compañía maximizar la cantidad de bienes que se pueden fabricar?
Solución
Sea
K = unidades de capital contratadas y
L = unidades de trabajo compradas
entonces K y L deben satisfacer
Por lo tanto, la compañía quiere resolver el siguiente problema de maximización restringido:
Problemas de programación no lineal.
En general en la resolución de un problema de programación no lineal seguiremos una serie de pasos:
En primer lugar intentaremos representar gráficamente nuestro conjunto de oportunidades y las curvas de nivel de la función objetivo.
El segundo paso consistirá en comprobar la aplicabilidad de los Teoremas de Weierstrass y Local – Global, de tal forma que podamos tener seguridad de la existencia de solución global a nuestro problema, y si dichas soluciones que obtengamos con las técnicas aplicadas son las soluciones globales.
En tercer lugar obtendremos las soluciones a nuestro problema mediante las condiciones de punto estacionario, aunque en este caso podemos seguir dos vías para la resolución del sistema que se genera. Una, corresponde a la resolución de dicho sistema teniendo en cuenta las distintas ramas que se presenten y otra, basada en la determinación, con la ayuda de la representación gráfica, de las restricciones activas en el óptimo y reducir de esa manera las distintas posibilidades del caso anterior.
Posteriormente deben analizarse las condiciones de segundo orden tanto necesaria como suficientes, para poder afirmar si dichos puntos estacionarios son óptimos, y si lo son, si son locales o globales.
El conjunto de oportunidades, como podemos observar en la gráfica, es un conjunto cerrado, acotado, convexo y no vacío, mientras que la función objetivo es continua y convexa, luego por el Teorema de Weierstrass podemos asegurar que existe un mínimo global y por el Teorema Local – Global, todo mínimo local es global.
En consecuencia, nos bastaría con determinar los mínimos locales y directamente obtendremos los globales pero, como se verifican las condiciones suficientes para que un punto estacionario sea mínimo global, sólo necesitamos encontrar los puntos estacionarios.
Para ello, podemos hacerlo de dos formas posibles, directamente a través de las condiciones de punto estacionario, o bien, a través de la gráfica analizando las restricciones activas en el mínimo. Veamos los dos procedimientos comenzando por el de punto estacionario.
Para resolver el problema a través de las condiciones de punto estacionario, para construir la función de Lagrange deberemos modificar nuestra función objetivo de acuerdo con la relación:
Min (x – 3)2 + (y – 1)2 = – Max – (x – 3)2 – (y – 1)2
Y entonces, la función de Lagrange vendrá dada por
L ( x, y, ë1 , ë2 ) = −( x − 3)− ( y − 1) 2− ë1 ( x+ y 2− 9) − ë2 ( 5 −5x + y)
Observemos que la segunda restricción ha debido adaptarse a la forma ≤.
Las condiciones de punto estacionario vienen dadas por:
El conjunto de oportunidades, como podemos observar en la gráfica, es un conjunto cerrado, acotado, convexo y no vacío, mientras que la función objetivo es continua y convexa, luego por el Teorema de Weierstrass podemos asegurar que existe un mínimo global y por el Teorema Local – Global, todo mínimo local es global.
En consecuencia, nos bastaría con determinar los mínimos locales y directamente obtendremos los globales pero, como se verifican las condiciones suficientes para que un punto estacionario sea mínimo global, sólo necesitamos encontrar los puntos estacionarios.
Para ello, podemos hacerlo de dos formas posibles, directamente a través de las condiciones de punto estacionario, o bien, a través de la gráfica analizando las restricciones activas en el mínimo. Veamos los dos procedimientos comenzando por el de punto estacionario.
Para resolver el problema a través de las condiciones de punto estacionario, para construir la función de Lagrange deberemos modificar nuestra función objetivo de acuerdo con la relación:
Min (x – 3)2 + (y – 1)2 = – Max – (x – 3)2 – (y – 1)2
Y entonces, la función de Lagrange vendrá dada por
L ( x, y, ë1 , ë2 ) = −( x − 3)
− ( y − 1) 2− ë1 ( x+ y 2− 9) − ë2 ( 5 − + y)
Observemos que la segunda restricción ha debido adaptarse a la forma ≤.
Las condiciones de punto estacionario vienen dadas por: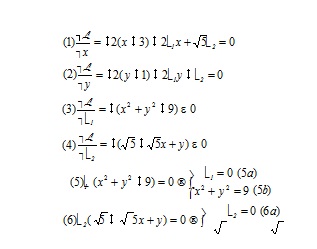
Para resolver ese sistema que contiene ecuaciones e inecuaciones comenzaremos resolviendo las ecuaciones y posteriormente, comprobaremos el cumplimiento de las inecuaciones. Así, determinaremos los puntos que verifican (1), (2), (5) y (6). Para ello, pueden formarse cuatro sistemas que vienen dados por las ecuaciones (1), (2), (5a) o (5b) y (6a) o (6b). Posteriormente, comprobaremos si las soluciones verifican las inecuaciones (3), (4), (7) y (8) y dichos puntos serán los puntos estacionarios para nuestro problema de mínimo.
Pasamos a estudiar cada una de las cuatro posibilidades que surgen al combinar las distintas ramas.
a) ë1 = ë2 = 0-2(x-3) = 0 ⇒ x = 3-2(y-1) = 0 ⇒ y = 1
Punto que no verifica la primera restricción luego no sería factible.
b) ë1 = 0 5 x + y = – 2( x − 3)-2(x-3) + 5 ë2 = 0 ⇒ë2 = 5-2(y-1) – ë2 = 0 ⇒ë2 = −2( y − 1)
Igualando las dos expresiones que surgen para ë2 y despejando la variable x
obtenemos que



La siguiente pregunta que debemos contestar para finalizar la resolución de este problema es si este punto estacionario es un mínimo global. La respuesta sería sí, ya que, como ya hemos visto, se verifican las condiciones suficientes para que un punto estacionario sea mínimo global







Comentarios»
No comments yet — be the first.